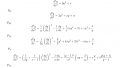前に書いたPDF「Hitchin可積分系」の紹介。
Hitchin可積分系
[2024/8/21]
すうがく徒のつどい(第6回)で発表することにしました。
発表原稿(英語版): Non abelian Hodge
発表原稿(日本語版): 非可換ホッジ理論
発表のアブストラクト: アブストラクト
Hitchin可積分系とは
コンパクトな非特異代数曲線 \( \Sigma \) について、その上の半安定ベクトル束のモジュライ空間 \( \mathcal{M}_{ \Sigma } \) を考える。
このモジュライ空間そのものでなく、余接束 \( T^{*}\mathcal{M}_{\Sigma} \) を見ると自然な代数的完全可積分系の構造が入っていることが示されている。
また、この余接束がパラメトライズしているものを「Higgs束」という。
余接束をコンパクト化したところまで考えることで、元のベクトル束の安定性を緩めた「(半)安定Higgs束」が定義される。これらのモジュライ空間が存在し、それをHitchin可積分系という。
特徴
「Higgs束」はベクトル束 \( E \) とHiggs場 \( \theta \in H^0(\Sigma,{\mathop{\mathrm{End}}\nolimits} E \otimes \omega_{\Sigma}) \) と呼ばれる要素のペアであるが、Higgs束はだいたい行列の道具で調べることができる。
Hitchin可積分系からHiggs場の特性多項式のなす空間に写像が構成でき(Hitchin fibration)、各ファイバーは特性多項式が定める代数曲線のヤコビ多様体になっている。
そのためコホモロジーの計算がしやすかったりする。
補足
参考にした論文(Donagi-Markman)では、このHitchin可積分系の解説のみならず、この可積分系と他の可積分系との繋がりを紹介していて面白い。
Hitchin可積分系について日本語で書かれた文献は殆どない。
最近出た寺杣先生の「リーマン面の理論」では、９章で少しだけ扱われている。題材は「Hichin可積分系」のものと同じだと思う。
もっとお話感覚の解説が下のツイートに貼ってある.
