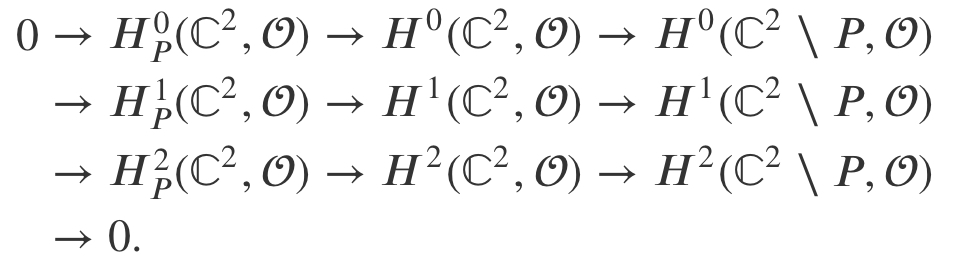\( \mathbb{C}^2 \setminus \{0 \} \)上の正則関数のなす層\( \mathcal{O}\)のコホモロジーを計算する。
① \(P := \{0 \} \)とおく。局所コホモロジー論により、次の長完全系列が得られる。
$$
\begin{equation}
\begin{split}
0 &\rightarrow H^0_P(\mathbb{C}^2, \mathcal{O}) \rightarrow H^0(\mathbb{C}^2, \mathcal{O}) \rightarrow H^0(\mathbb{C}^2 \setminus P, \mathcal{O})\\
&\rightarrow H_P^1(\mathbb{C}^2, \mathcal{O}) \rightarrow H^1(\mathbb{C}^2, \mathcal{O}) \rightarrow H^1(\mathbb{C}^2 \setminus P, \mathcal{O})\\
&\rightarrow H_P^2(\mathbb{C}^2, \mathcal{O}) \rightarrow H^2(\mathbb{C}^2, \mathcal{O}) \rightarrow H^2(\mathbb{C}^2 \setminus P, \mathcal{O})\\
&\rightarrow 0.
\end{split}
\end{equation}
$$
ここで\( H^i(\mathbb{C}^2, \mathcal{O}) = 0 \) (\( i > 0\))、 \(H^i_P(\mathbb{C}^2, \mathcal{O}) = 0\) (\(i > 2\))であり、
ハルトークスの定理から\(H^0(\mathbb{C}^2, \mathcal{O}) \xrightarrow{\sim} H^0(\mathbb{C}^2 \setminus P, \mathcal{O})\) である。よって
$$
\begin{equation}
\begin{split}
H^0(\mathbb{C}^2 \setminus P, \mathcal{O}) &=H^0(\mathbb{C}^2, \mathcal{O}),\ (i = 0),\\
H^1(\mathbb{C}^2 \setminus P, \mathcal{O}) &= H^2_P(\mathbb{C}^2, \mathcal{O}), \ (i = 1),\\
H^i(\mathbb{C}^2 \setminus P, \mathcal{O}) &= 0, \ (i > 1).
\end{split}
\end{equation}
$$
② \( H^1(\mathbb{C}^2 \setminus P, \mathcal{O})\)について詳しく調べる。
\( U_1 := \mathbb{C}^2 \setminus \{z_1 = 0 \} = \{z_1 \neq 0 \}\)、 \(U_2 := \mathbb{C}^2 \setminus \{z_2 = 0 \} = \{z_2 \neq 0 \}\)とおく。
\(U_1 \cup U_2 = \mathbb{C}^2 \setminus P\)、\(U_1 \cap U_2 \simeq \mathbb{C}^* \times \mathbb{C}^* \)、\(U_1 \simeq U_2 \simeq \mathbb{C} \times \mathbb{C}^* \)なので
\(i > 0\)について\(H^i(U_1,\mathcal{O}) = 0\)、\(H^i(U_2, \mathcal{O})=0\)、\(H^i(U_1 \cap U_2, \mathcal{O}) = 0\)。
つまり\( \mathcal{U} := \{U_1, U_2 \}\) はacyclic cover であり、\(H^i(\mathbb{C}^2 \setminus P, \mathcal{O}) \simeq H^i(\mathcal{U}, \mathcal{O})\)。
今、1-cochain、つまり\(C^1(\mathcal{U}, \mathcal{O}) = \mathcal{O}(U_1 \cap U_2)\)の元は
$$f(z_1, z_2) = \sum_{m, n = -\infty}^{\infty} a_{m, n} z_1^m z_2^n
$$
と表せる。
また、\(\mathcal{O}(U_1)\)の元は \(f(z_1, z_2) = \sum_{n \geq 0} b_{m, n}z_1^m z_2^n\)、\(\mathcal{O}(U_2)\)の元は\(f(z_1, z_2) = \sum_{m \geq 0} z_1^mz_2^n\)と表せる。よって
$$\delta(\mathcal{C}^0(\mathcal{U}, \mathcal{O})) = \mathcal{O}(U_1) + \mathcal{O}(U_2).
$$
以上から、\(H^1(\mathbb{C}^2 \setminus P, \mathcal{O})\)は\(z_1^mz_2^n\) \( (m, n < 0)\)で張られる無限次元ベクトル空間である
(\(\dim_{\mathbb{C}} H^1(\mathbb{C}^2 \setminus P, \mathcal{O}) = \infty\))。
③ ここで\(\mathfrak{m}_P\) を、\(P\)に対応する\(A := \mathbb{C}[z_1, z_2]\)の極大イデアルとする。 \(\mathbb{C}^2 = \mathop{\rm Spec}\nolimits (\mathbb{C}[z_1, z_2]) = \mathop{\rm Spec}\nolimits(A)\)であり、
$$
\begin{equation}
\begin{split}
H_P^2(\mathbb{C}^2, \mathcal{O})
&\simeq H_{\mathfrak{m}_P}^2(A)\\
&\simeq \varinjlim_{k} \mathop{\rm Ext}\nolimits^2(\mathcal{O}/\mathfrak{m}_P^k, \mathcal{O})\\
&\simeq \varinjlim_kH^0(P, \mathcal{E}xt^2(\mathcal{O}/\mathfrak{m}_P^k, \mathcal{O})).
\end{split}
\end{equation}
$$
次の層単完全系列を考える。
$$
\begin{equation}
0 \rightarrow \mathfrak{m}_P^k/\mathfrak{m}_P^{k + 1} \rightarrow \mathcal{O}/\mathfrak{m}_P^{k + 1} \rightarrow \mathcal{O}/\mathfrak{m}_P^k \rightarrow 0. \end{equation}
$$
また、\( \mathfrak{m}_P^k/\mathfrak{m}_P^{k + 1} \simeq (\mathfrak{m}_P/\mathfrak{m}_P^2)^k\)である。これより、次の長完全系列を得る。
$$
\begin{equation}
\begin{split}
0 &\rightarrow \mathcal{E}xt^0(\mathcal{O}/\mathfrak{m}_P^{k}, \mathcal{O}) \rightarrow \mathcal{E}xt^0(\mathcal{O}/\mathfrak{m}_P^{k+1}, \mathcal{O}) \rightarrow \mathcal{E}xt^0((\mathfrak{m}_P/\mathfrak{m}_P^2)^k, \mathcal{O})\\
&\rightarrow \mathcal{E}xt^1(\mathcal{O}/\mathfrak{m}_P^{k}, \mathcal{O}) \rightarrow \mathcal{E}xt^1(\mathcal{O}/\mathfrak{m}_P^{k+1}, \mathcal{O}) \rightarrow \mathcal{E}xt^1((\mathfrak{m}_P/\mathfrak{m}_P^2)^k, \mathcal{O})\\
&\rightarrow \mathcal{E}xt^2(\mathcal{O}/\mathfrak{m}_P^{k}, \mathcal{O}) \rightarrow \mathcal{E}xt^2(\mathcal{O}/\mathfrak{m}_P^{k+1}, \mathcal{O}) \rightarrow \mathcal{E}xt^2((\mathfrak{m}_P/\mathfrak{m}_P^2)^k, \mathcal{O})\\
&\rightarrow 0.
\end{split}
\end{equation}
$$
\(\mathop{\rm codim}\nolimits_P(\mathbb{C}^2) = 2\)より、
$$
\begin{equation}
0 \rightarrow \mathcal{E}xt^2(\mathcal{O}/\mathfrak{m}_P^{k}, \mathcal{O}) \rightarrow \mathcal{E}xt^2(\mathcal{O}/\mathfrak{m}_P^{k+1}, \mathcal{O}) \rightarrow \mathcal{E}xt^2((\mathfrak{m}_P/\mathfrak{m}_P^2)^k, \mathcal{O}) \rightarrow 0.
\end{equation}
$$
よって、\(H_P^2(\mathbb{C}^2, \mathcal{O})\)には、フィルトレーション\(\{H^0(P, \mathcal{E}xt^2((\mathfrak{m}_P/\mathfrak{m}_P^2)^k, \mathcal{O})) \}_k\)がある。 (ひとつひとつは\(\langle z_1^mz_2^n\rangle_{m + n =-k,\ m, n <0} \)に対応すると思うが、まだ確認していない)
[追記 2020/11/13]
ワヘイヘイさん(@waheyhey)に \( \mathbb{C}^2 \) の \( P:= \{0 \} \) におけるブローアップを考えることで \(H^i(\mathbb{C}^2 \setminus P, \mathcal{O}) \) を計算する方法を教えて頂いたので追記します。
\(X \) を \( \mathbb{C}^2 \) の \( P\) におけるブローアップ、\( E\) をブローアップにおける例外曲線、\( U := \mathbb{C}^2 \setminus P\)、\( j : U \hookrightarrow X\) を開埋め込みとする。
このとき、層の短完全系列
$$
\begin{equation}
0 \rightarrow \mathcal{O}_{X} \rightarrow j_*\mathcal{O}_U \rightarrow \bigoplus_{k = 1}^{\infty} \mathcal{O}_E(-k)\rightarrow 0 \end{equation}
$$
があり、これにより次のコホモロジー長完全系列を得る：
$$
\begin{equation}
\begin{split}
0 &\rightarrow H^0(X, \mathcal{O}_X) \rightarrow H^0(X, j_*\mathcal{O}_U) \rightarrow H^0(E, \oplus_{k = 1}^{\infty} \mathcal{O}_E(-k))\\
&\rightarrow H^1(X, \mathcal{O}_X) \rightarrow H^1(X, j_*\mathcal{O}_U) \rightarrow H^1(E, \oplus_{k = 1}^{\infty} \mathcal{O}_E(-k))\\
&\rightarrow H^2(X, \mathcal{O}_X) \rightarrow H^2(X, j_*\mathcal{O}_U) \rightarrow 0.\end{split}
\end{equation}
$$
ここで \( H^i(X, \mathcal{O}_X) \simeq H^i(\mathbb{C}^2, \mathcal{O})\) であり、また \( j\) はアフィン射なので \( H^i(X, j_*\mathcal{O}_U) \simeq H^i(U, \mathcal{O}_U)\) であることも分かる。
ゆえに、長完全系列から
$$H^1(U, \mathcal{O}_U) \simeq \bigoplus_{k = 1}^{\infty} H^1(E, \mathcal{O}_E(-k))$$
を得る。
①③での議論により、
$$ H_P^2(\mathbb{C}^2, \mathcal{O}) \simeq\varinjlim_kH^0(P, \mathcal{E}xt^2(\mathcal{O}/\mathfrak{m}_P^k, \mathcal{O})) \simeq \bigoplus_{k = 1}^{\infty} H^1(E, \mathcal{O}_E(-k))$$
である。
③におけるフィルトレーション\(\{H^0(P, \mathcal{E}xt^2((\mathfrak{m}_P/\mathfrak{m}_P^2)^k, \mathcal{O})) \}_k\)の構造から、同型
$$ H^0(P, \mathcal{E}xt^2((\mathfrak{m}_P/\mathfrak{m}_P^2)^k, \mathcal{O})) \simeq H^1(E, \mathcal{O}_E(-k))$$
が予想される(まだ示せていないので、分かる方は教えて下さい)。
