ラングランズ対応の紹介を簡単に行います。
ラングランズ対応とは
数学の世界には、大雑把に分けて３つの分野があります。
代数学、幾何学、解析学です。
おそらく、この記事を読んでいる方はフェルマーの最終定理について名前くらいは聞いたことがあると思います。
このフェルマーの最終定理は代数学の世界に属する定理で、1994年にAndrew Wiles が証明するまで360年間未解決でした。
Wilesによる証明の鍵となったのが「志村・谷山予想」と「Ribetのレベル下げ定理」でした。
特に「志村・谷山予想」についてですが、この定理によって代数の世界と解析の世界との間に橋が架けられます。
このように、数学の様々な分野の架け橋となるような理論の一つとして「ラングランズ予想」があります。
分野を繋げて何が嬉しいんだろう？と思う方もいるかも知れません。
例えばフェルマーの最終定理の場合、Wilesは代数学の非常に難しい問題を「志村・谷山予想(今は定理)」を用いて解析学の問題に翻訳しました。
この場合、翻訳してできた問題が元の問題よりも簡単だったため、解決することができたのです。
このような事例は「ミラー対称性」についても言えます。
(ミラー対称性の主張についてはコチラも参照)
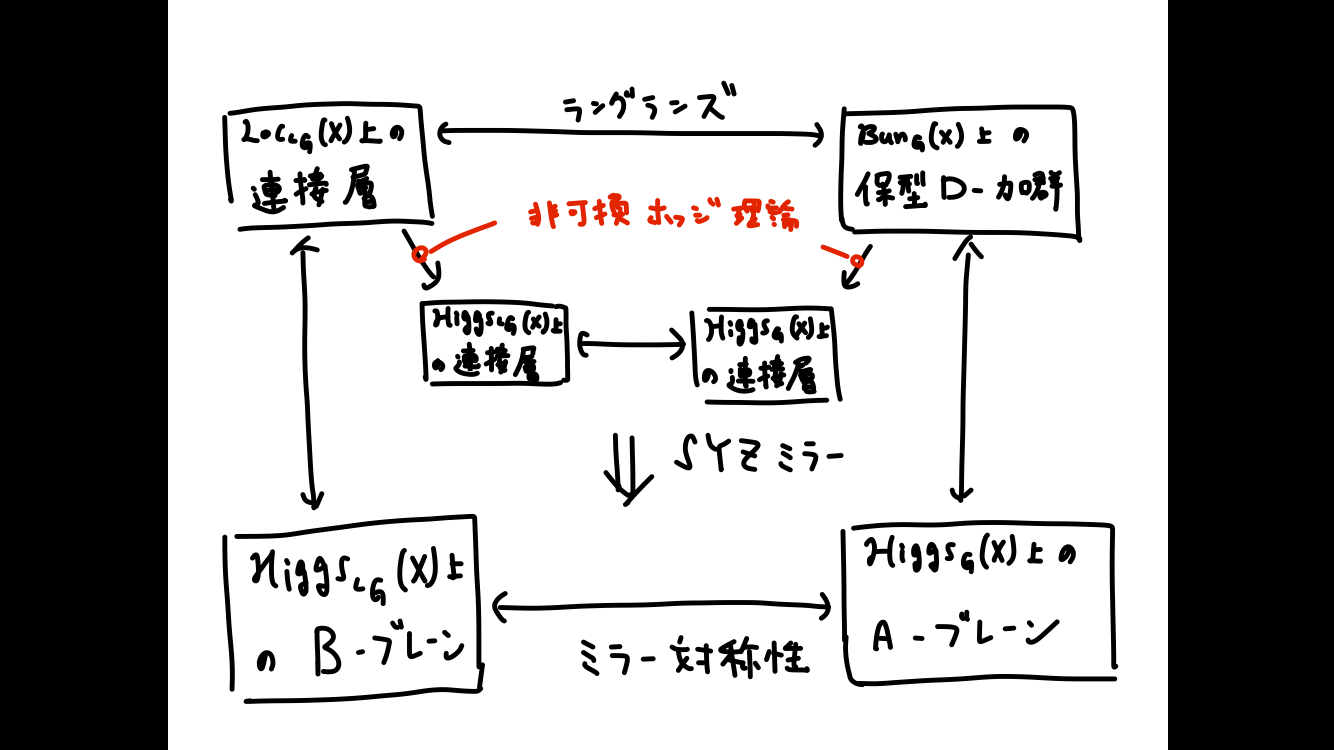
幾何学的ラングランズ対応
先に述べたラングランズ対応は、数論(代数学の一分野)的ラングランズ対応と呼ばれるものです。
この予想を幾何学の言葉に翻訳したものとして幾何学的ラングランズ対応があります。
(解析学へ翻訳したものは関数体上のラングランズ対応？？どれも代数学のような気がする…)
もう少し詳しく知りたい方は下の「高校生のときに聞きたかった話」の記事を読んでください。
もっと知りたい方のために
E. Frenkelさんの一般向け著書「数学の大統一に挑む」を是非読んでください。
ラングランズ予想の専門家であるFrenkelさんが一般の人にも分かりやすく解説してくれています。
ちなみに原題は「Love and Math」(さすがFrenkelさん)
E. Frenkelの公式チャンネルにNHK白熱教室の動画があります。
この番組はFrenkelさんの「数学の大統一に挑む」の出版を受けて作成されたものです。全4回。
より専門的に知りたい方はコチラ。
