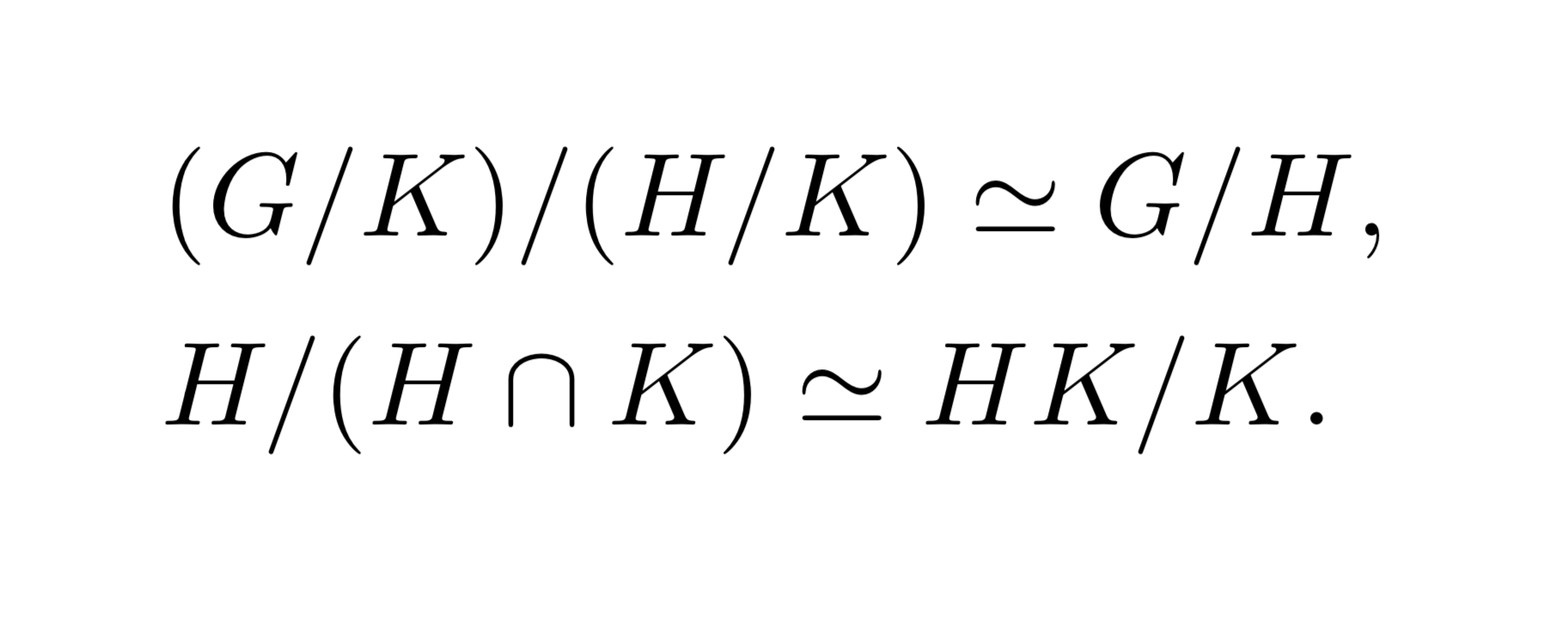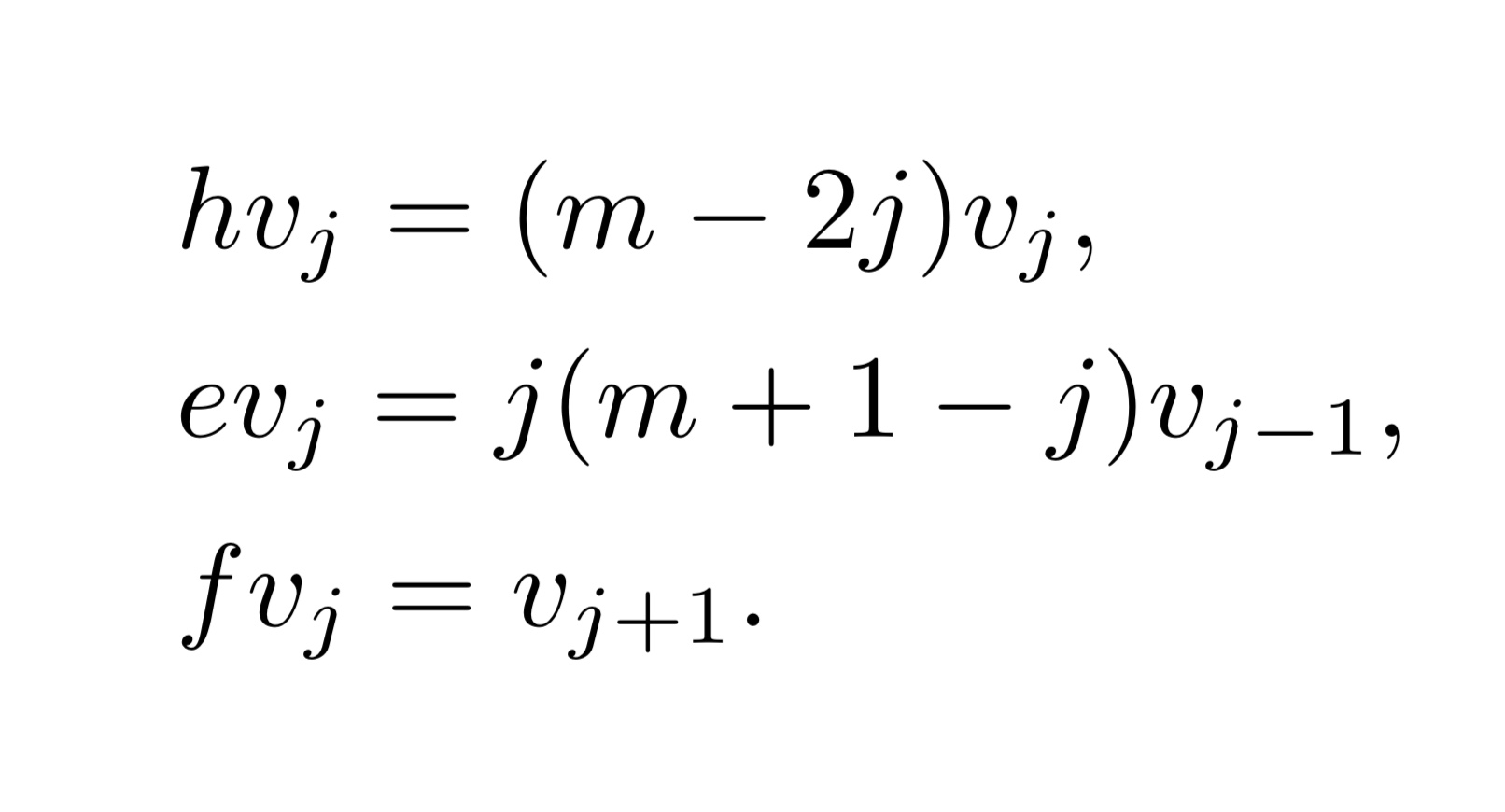群論は数学における基礎的な概念なので、代数/幾何/解析の分野に関わらず、あるいは数学に限らず、様々な場面で登場する。
将来的に何をするにせよ、群論の考え方を身につけることは大切である。
数学ガール フェルマーの最終定理
結城先生の「数学ガール」 特に第2巻の「フェルマーの最終定理」
大学数学の勉強を始めたばかりの人にとって、群の定義は無味乾燥に見えると思う。
この本では、登場人物であるミルカさんやテトラちゃん、主人公である僕が対話をする中で群の定義の意味するところを紐解いていく。
彼らの思考を追体験することにより、群の定義に自然と慣れ親しむことができるのではないかと思う。
群・環・体 入門
とにかく速習したい人向け。
対称性からの群論入門
M. A. アームストロング著「対称性からの群論入門」
初めて群論を勉強する人は、まずこの本を眺めてみると良いと思う。
教科書というよりも、読み物として読んで折に触れて読み返すのをオススメする。
具体例が豊富で、群の扱いや考え方が自然と身につくようになっている。
どの分野を勉強するにしても、具体例が頭に入っているのといないのとでは理解度に格段の差が出ると思う。
「佐藤先生のホームページ」に正誤表がある。
代数学1 群論入門 (雪江 明彦著 日本評論社)
雪江先生の「群論入門」
この本を読んでいる人が多いように思う。
解説や記述が丁寧で行間が少ない。
なので独学だったり、授業前に予習したりするのにおすすめ。
特に“well-defined”など初学者には掴みづらい概念を丁寧に解説している点が良い。
「雪江先生のホームページ」に正誤表がある。
代数学1 群と環 (桂 利行著 東京大学出版)
桂先生の「群と環」
考察や「(所謂)気持ち」の部分が殆ど無く、全体的にスッキリまとまっている。
個人的にはこの本が好き。
授業で聞いた後や、大学院に上がった後に復習するのにおすすめ。
現代数学18 群論 上下 (鈴木 道夫著 岩波書店)
鈴木先生の「群論」
より専門的に学びたい人向け。
研究するとき、分からない概念を調べるために手元に置いている。
GTM211 Algebra (S. Lang著 Springer)
S. Langの「Algebra」
群論を洋書で勉強することも良いと思う。
授業や勉強が進んでいく度に対応する箇所を確認して、英語だとどのように表現するのか見てみるのもオススメ。
その他有名なもの
岩波講座 現代数学の基礎「群論」寺田・原田