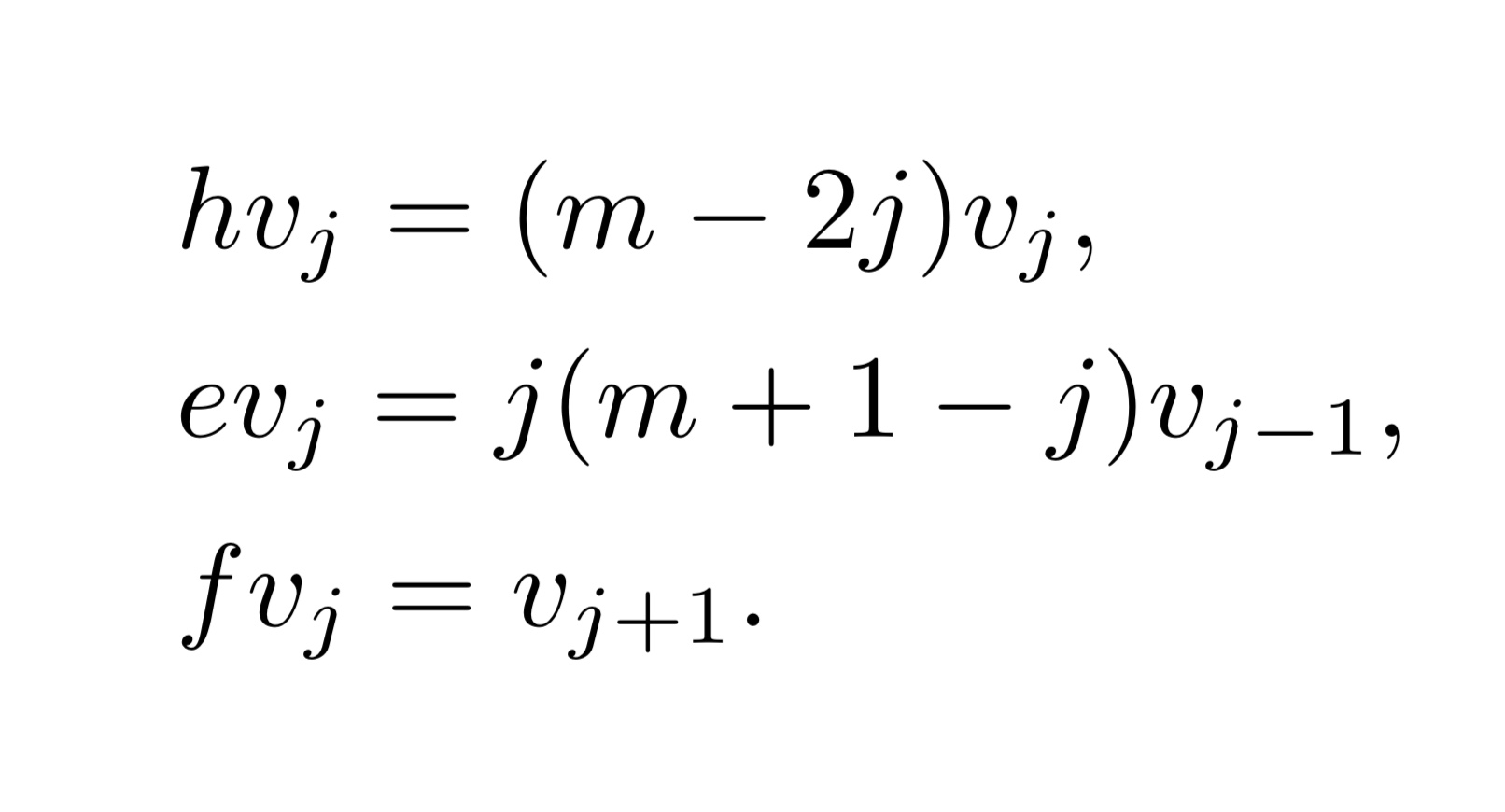リー代数は至るところに現れるが、それはリー群が至るところに現れるから。リー群が至るところに現れるのは、群が至るところに現れるから…というか、群(対称性)の作用があると研究しやすいから。(だと今のところ理解している。そのうち変わることもあるかも。)
はじめに
最初はリー代数についてだけ書こうと思ったが、リー代数の話を始めるにあたってリー群の話抜きでは難しそうだったのでリー群も加えた。
リー代数を大雑把に説明すると、連続群(リー群)を無限小(単位元の近く)で見たものである。
またリー群とは、多様体であって群をなすものである。
リー群を直接調べるのは少し難しいので、単位元の近くだけに注目して考える。
そうすることでリー群のことがいっぱい分かる。
例えば高校数学で3次曲線や4次曲線を調べるとき、直接考えてもよく分からないが微分して接線を調べると元の曲線のことがよく分かった。
やっていることはあまり変わらない。
ただ、接線(1次元)と違って次元が大きくなるので、線形代数の道具を使って調べることになる。
リー群の話
佐武先生の「リー群の話」
教科書というより、読み物として読むタイプの本。
行列のリー群を使って、リー群やリー代数が何なのか、何を調べるのか、どういう事柄と関連しているのかを説明している。
数式を一つ一つ確認するのは無理だと思うので、まぁそんなもんか、くらいで読み進めれば良いと思う。
多様体入門 (松島 与三著 裳華房)
松島先生の「多様体入門」
色んな意見を見るものの、やはり多様体の名著。
4章が「リイ群と等質空間」である(リー群=多様体+群)。
ありがたいことに「2016/自主ゼミ/松島多様体」に正誤表がある。
新装版が出て(物理的に)読みやすくなった。
なんとなく拒否反応が出る人はWarnerを読むと良いと思う。
(2021/10/28 追記 多様体の基礎を傍らに置きつつトゥー多様体を読むと良い)
リー代数入門 -線形代数の続編として-
佐藤肇先生の「リー代数入門」
3×3行列などで具体的に計算して理解を深める本。
この小さな本の目的は、リー代数(リー環とも呼ばれる)の理論を、具体的に、たくさんの例を調べることにより、やさしく身につけて、手っとり早く応用できるようにすることである。
リー代数入門-線形代数の続編として- はじめに(iii)
例えばKilling形式など、定義だけ見ても何を定義したのかよく分からない、ということがある。
そういう概念も、具体例で計算することによって使える道具になっていく。
ただ、この本だけでリー代数に入門しようとすると(計算練習ばかりになるので)リー代数の面白味が半減するかも。
下にある教科書で理論を学ぶときに、一緒に読むのがオススメ。
リー環の話
佐武先生の「リー環の話」
「リー群の話」と違って、こちらは教科書の体裁で書かれている。
丁寧に書かれている印象があり、リー代数の基本的な知識は十分に身につく。
誤字脱字は多少気になるが、内容の理解には影響無いと思う。
Introduction to Lie algebras and Representation Theory
Humphreysの「Introduction to Lie Algebras and Representation Theory 」
佐武先生の「リー環の話」は、この前半部分を参考にして書いているようである。
この本を読めば(分野にも依るが)論文を読み始めることもできると思う。
ページ数の割に内容が多いので、所々行間の広いところがある。
前半部分は「リー環の話」と合わせて読めば理解が深まる。
ところで、リー代数の分類理論では「ルート系」が活躍する。
例えばそこで使われる「ワイル群」は単なる鏡写し(鏡映変換)なのだが、数式だけ見て考えていると何をやっているのか分からなくなるかもしれない(僕はなった…)。
「鏡映の数学」や「不変量と対称性」の4章などで鏡映群に慣れておくと良いと思う。
無限次元リー環
脇本先生の「無限次元リー環」
有限次元のリー代数やその表現論に慣れるために、一度無限次元の世界を見ておくのも良いかもしれない。
無限次元に興味が無くても、一度手にとって見て28、29ページを読んで欲しい。
脇本先生の、\( \mathfrak{s}l_2(\mathbb{C})\)への愛が溢れ出している。
Infinite dimensional Lie algebras
無限次元リー代数の創始者Kac先生の「Infinite dimensional Lie algebras」
本格的に無限次元リー代数を使うのであれば読むべき本。
脇本先生の本は、この本へのガイド・ブックとして書かれたものらしい。
(まだちゃんと読めていないので何とも言えない…索引が無いのがちょっと不便だなぁと思う)
その他:気になる本
「リー代数と量子群 」