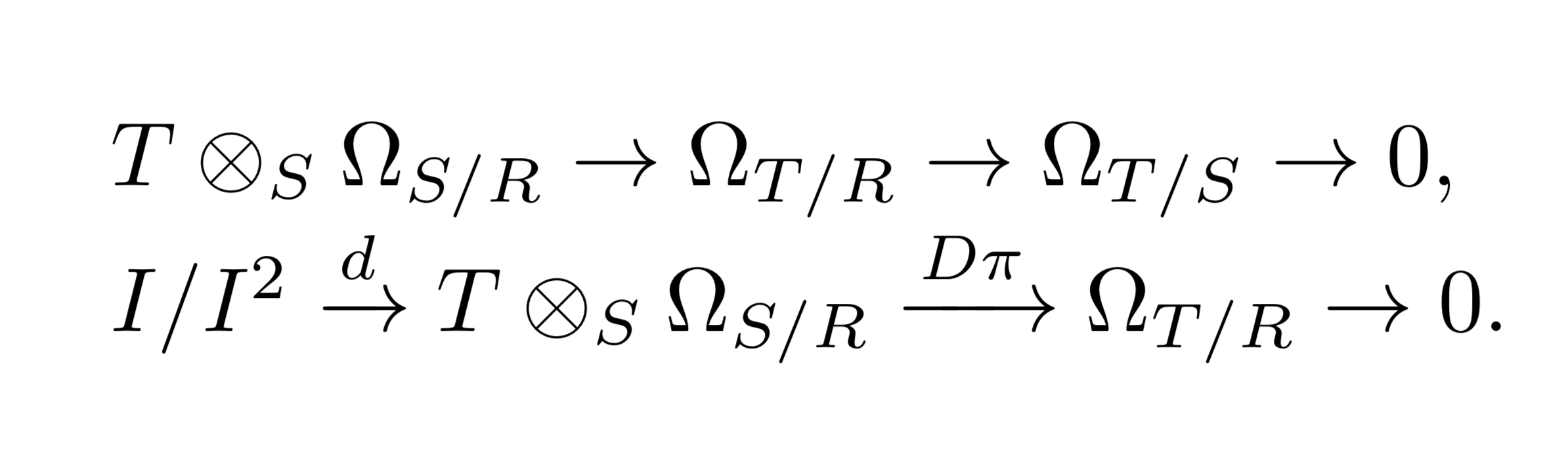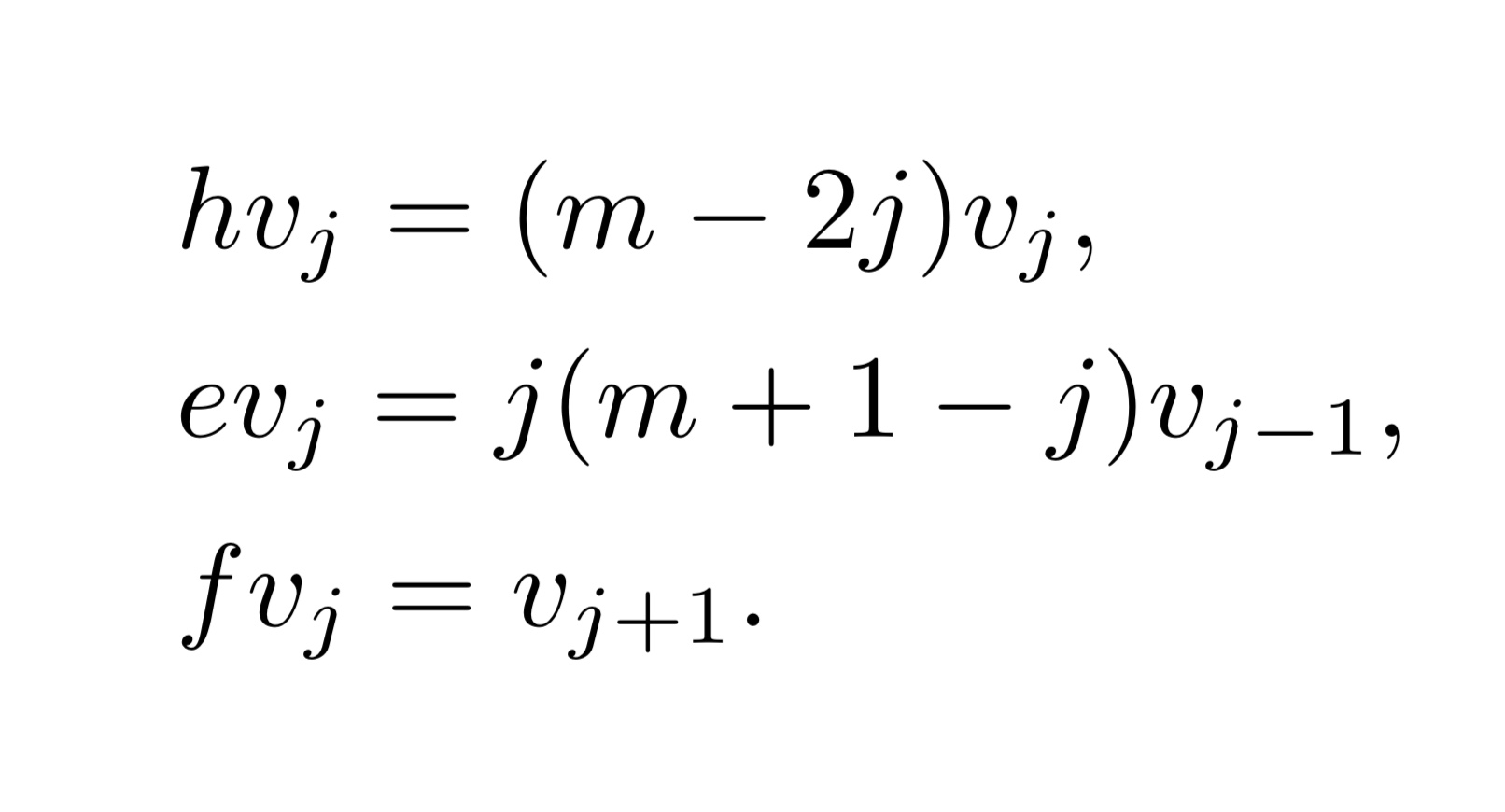ここでは、代数幾何学を念頭に置いて紹介を行う。
代数学2 環と体とガロア理論
雪江先生の「環と体とガロア理論」
授業の予習復習にせよ、独学にせよ、まずはこの本を読んでみることをオススメする。
必要な事柄がおおよそ書かれているし、例題も演習問題も豊富。
個人的に気に入っている点は「1.9 可換環と代数幾何」の節で可換環と代数幾何学との関係を簡単に説明していて、
点 ↔ 素イデアル
近傍 ↔ 環の局所化
方程式の零点 ↔ イデアル
代数的な写像 ↔ 環準同型
の対応が書かれているところである。
このことは代数幾何を勉強している人にとっては“常識”なので、いちいち纏めて説明されることは意外と少ない。
この本ではその辺りの雰囲気を教えてくれ、代数幾何を勉強するときの良いモチベーションとなるだろう。
「雪江先生のホームページ」に正誤表がある。
可換環論入門
M. Reidの「可換環論入門」
可換環の教科書というと多くの人がアティヤ・マクドナルドをまず読み始める印象がある。
こちらの本は図がたくさん使われているし、全体的に読みやすい印象がある。
というか、読んでて面白い(0章 こんにちは! 9章 さようなら!)。
内容としてはアティヤ・マクドナルドの1〜8章とほぼ同じ。
アティマクが合わない人は、この本を読んでみると良いと思う。
この本だけでは、代数幾何学を勉強するのに必要な知識が十分補えるとは言えないので、下の本たちも続けて読むべきである。
可換環と体
堀田先生の「可換環と体」(元は現代数学の基礎 環と体 1.2)
個人的にはこの本が好き。
アティヤ・マクドナルドにはないCohen-Macaulay加群の章もある。
説明も丁寧で分かりやすく、もっと人気が出ても良いのになぁと思っている。
後半の体論も面白く、最終章ではWeil予想についても触れられている。
Atiyah‐MacDonald 可換代数入門
アティヤ・マクドナルド「可換代数入門」
このページを見ている人なら「アティマク」の名を一度は目にしたことがあると思う。
代数幾何学に必要な可換環の知識を手っ取り早く得るには、この本を読むのが一番。
演習問題が非常に多いことで有名。
「atiyah, macdonald, solutions」で検索すれば解答例がいっぱい出てくる。
初めて読むときには、とりあえず演習問題は置いておいて、先に全体像を掴んだほうが良いと思う。
ときどき現れる変な日本語はご愛嬌。
10章はどうも読みにくい気がするので、他の本も併用して勉強すると良い。
(これは10章の中に線形位相、完備化、次数付き環、フィルター加群、と多くのトピックが詰め込まれているためだと思う。それぞれ個別に勉強することをオススメする。
例えば谷崎先生の非可換環は次数付き環やフィルター加群に詳しい。)
可換環論 (Commutative Ring Theory)
松村先生の「可換環論」あるいはM. Riedさんによって翻訳された「Commutative Ring Theory」
代数幾何学を勉強していると、どうしてもこの本に書いてあることまで必要になってくる。
これまでに挙げた本は可換環論の入門書だが、この本は専門書である。
つまり、一度可換環論の初歩を勉強していることを前提として書かれている。
そのため、初学者には難しい記述が多いと思われる。
Riedさんによって翻訳された英語版では一部の証明の記述が分かりやすくなっているところもあり、
そちらも合わせて読むことをオススメする。
なおハーツホーンで繰り返し引用されている「Matsumura」は別の本(Commutative Algebra)である。
現在ではCommutative Algebra をLaTeXで書き直したものがGitHub上に存在している。
内容を比べてみると、可換環論の方はCommutative Algebra を基礎にしてより内容が豊富になったものであると言える。
Commutative Algebra: with a View Toward Algebraic Geometry
D. Eisenbudの「Commutative Algebra」
松村本の代わりにこちらを読むことが多い。
少なくとも、読んだところについては分かりやすかった。
タイトル通り、代数幾何との繋がりについても説明してくれているので有り難い。
800ページ近くあるので、通して読むというよりも辞書のように使っている。
おまけ:ホモロジー代数
河田先生の「ホモロジー代数」
可換環論の本ではなくホモロジー代数の本だが、ここに載せておく。
可換環を勉強するときにも完全系列の知識は必要だし、代数幾何学では縦横無尽に使われる。
ホモロジー代数の勉強にはこの本が一番良いと思う。
しかし残念なことに、長らく絶版となっている。
(復刊しました。岩波書店さんありがとうございました。)
図書館で借りられれば良いが、難しい場合は志甫先生の「層とホモロジー代数」でももちろん大丈夫。